📈 #28 ¿Quién es influencer… Según la teoría de grafos?
Mitos y verdades sobre el número de seguidores.
¿Qué tienen en común las cuentas de Twitter/X de Cristiano Ronaldo, Justin Bieber, Barack Obama y Elon Musk?
Exacto: son las 4 cuentas de Twitter con más seguidores. Más de 100 millones cada una de ellas.
Cuando vi esas cifras, lo primero que pensé fue “uf, ¿llegaré yo algún día a ese número de seguidores?”.
A ver, hay una probabilidad prácticamente nula de que ocurra eso.
Pero lo siguiente que pensé fue “¿podría escribir un tweet que tuviese más likes que los suyos?”.
Y ahí fue donde sí vi una posibilidad. No sé si muy alta o muy baja, pero ahí está.
Porque me puse a indagar.
Es curioso, pero ni Cristiano ni Justin Bieber tienen tweets en el Top 20. Vamos, que no llegan al medio millón de likes. En cambio, entre tweets con tantos likes lo que sí vi fue uno con casi 3 millones de likes.
Uno de alguien que quizás no te esperes.
Uno de una cuenta que no llega al millón de seguidores.
Uno de…
Efectivamente, Macaulay Culkin.
No sé si estaba solo en casa o no cuando escribió el tweet, pero este de agosto de 2020 le valió para tener casi 3 millones de likes:
Solemos pensar que los influencers son aquellos que tienen más seguidores, pero está claro que no siempre es así.
Así que lo siguiente que se me vino a la cabeza fueron muchas preguntas.
¿Es el número de seguidores lo único que importa en una red social para volverse viral? ¿Es la manera en la que se distribuye la información? ¿Son los algoritmos los que lo manejan todo?
Hoy, en Factibles, te cuento cómo la Investigación Operativa da respuesta a estas preguntas a través de la teoría de grafos:
Qué es una red social
Qué podemos considerar un influencer según esta teoría
Cómo los negocios están muy impregnados de esta teoría (aunque no lo sepan)
Vamos a por ello!
🕸️ Redes sociales como grafos
Una red social como Twitter tiene, principalmente, dos cosas:
Usuarios
Relaciones entre ellos
Y no solo Twitter, claro. También LinkedIn, Instagram, Facebook o TikTok.
Por eso, toda red social se puede definir como un grafo: los nodos del grafo serían los usuarios que la componen, mientras que los arcos serían las relaciones existentes entre los nodos. Gráficamente, la podemos ver así:
Dependiendo de si las relaciones entre usuarios son simétricas o no, las relaciones se pintan con líneas o flechas, respectivamente.
En una red social con relaciones simétricas ocurre que los usuarios se siguen siempre mutuamente entre sí, como por ejemplo en Facebook o whatsapp. Esto se conoce como grafo no dirigido y las relaciones entre los usuarios se pintan con líneas.
En cambio, en una red social con relaciones asimétricas los usuarios no se tienen por qué seguir entre sí, como ocurre en Twitter o Instagram. En este caso el grafo es dirigido y las relaciones entre usuarios se pintan con flechas indicando quién sigue a quién.
Esto, que parece una tontería, es la base sobre la que se sustenta la forma en la que los mensajes se distribuyen en la red. Dependiendo de las relaciones que haya entre sus miembros, quién lance el mensaje, o cómo esté posicionado dentro de la red, los mensajes se distribuirán más rápidamente o menos.
Y es precisamente ese mecanismo de distribución de mensajes el que da pie al siguiente concepto: la viralidad y, más importante, la influencia de ciertos nodos de la red (o usuarios de la red social) para que un mensaje se distribuya y tenga muchas visitas y likes.
📸 Influencers desde la teoría de grafos
Los influencers de una red social son como los más populares del instituto, aquellas personas con las que todo el mundo quería estar. Gente importante.
Como tal, dentro de la red social también son importantes. De hecho, serán los nodos más importantes de la red.
Pero hemos visto un poco más arriba cuentas con cientos de millones de seguidores que no tienen muchos likes. Es más, ni los verás en el Top 20, cuando otros, con menos de 1 millón de seguidores, están ahí.
Entonces, ¿cómo podemos definir la importancia de un nodo de la red?
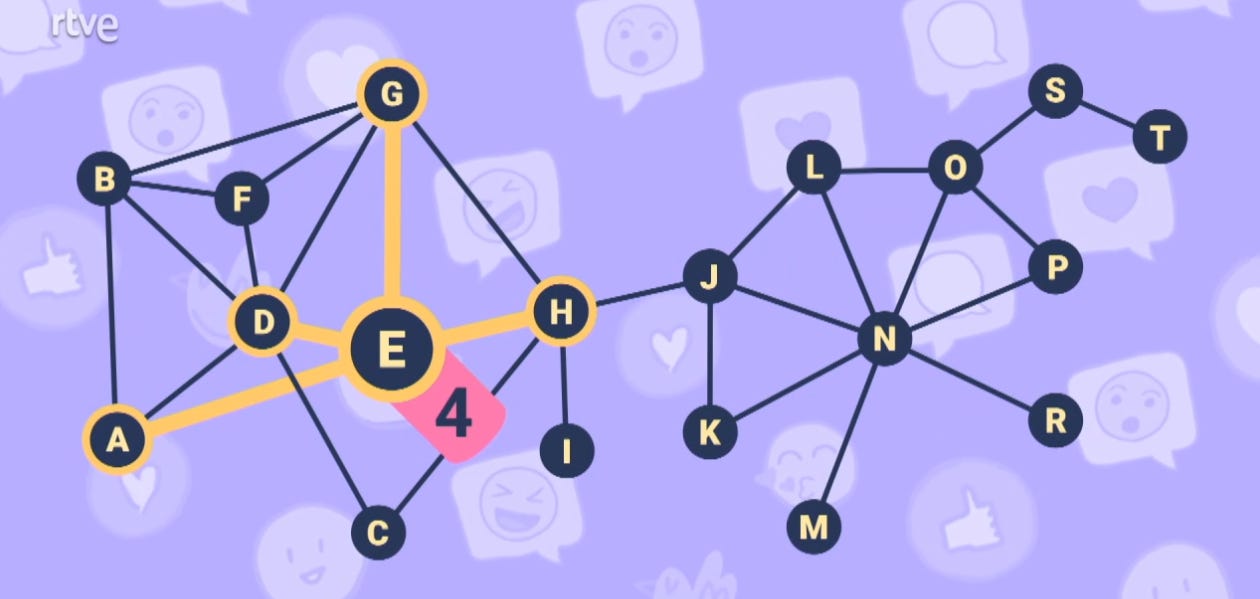
Uno de los conceptos básicos en teoría de grafos es la valencia de un nodo, que no es más que el número de conexiones que tiene el nodo. Por ejemplo, el nodo E tendría valencia 4 en este grafo porque tiene conexiones con 4 nodos adyacentes (A, D, G y H):
Con esto ya podemos calcular la valencia de cualquier nodo de la red y empezar a determinar la importancia de cada nodo:
Una primera propuesta para identificar el nodo más influyente sería quedarnos con el de mayor valencia, ¿verdad? Porque es el nodo que más contactos directos tiene. En este caso, nodo N es el de mayor valencia de toda la red:
¿Sería el nodo N el más importante de la red? Pues igual no… ¿Qué es más importante: tener muchos contactos, o que tus contactos tengan muchos contactos a su vez? El potencial de llegar a más gente es mayor en este segundo caso. Y siendo así, el mejor nodo para esto no sería el N sino el D: la suma de las valencias de sus contactos es 21, mientras que la suma de las valencias de los contactos del nodo N es 17:
Por lo que los mensajes que mande el nodo D potencialmente se propagrán con más facilidad por la red que los que mande el nodo N, a pesar de tener más contactos directos.
Eso sí, yo miro el grafo y veo un grave problema en el nodo D: si quiere mandar un mensaje al nodo T, le cuesta 7 saltos llegar a él.
En cambio, al nodo L solo le cuesta 3 saltos, y llegar al nodo más alejado de la red para él, el B, le cuesta 4 saltos. Es decir, el nodo L está mejor posicionado si queremos minimizar el número de saltos que tiene que dar un mensaje por la red:
Por lo que la propagación de un mensaje parece más rápida si se hace desde el nodo L que si se hace desde el nodo D.
No sé si te has dado cuenta, pero por la forma que tiene el grafo hay dos nodos concretamente que parecen importantes.
Vuelve a mirar cualquiera de las imágenes anteriores.
Lo ves, ¿no?
Los nodos H y J igual tienen algo que decir en todo esto. Si no comparten mensajes entre sí, esos mensajes no llegan al otro lado de la red. Son nodos que conectan comunidades diferentes, por lo que tienen un gran peso dentro del grafo:
Así que te devuelvo la pregunta: ¿quién dirías ahora que es influencer dentro de una red social?
💼 Teoría de grafos en problemas de negocios
La teoría de grafos, como ves, es súper útil al analizar redes sociales.
Y solo hemos rascado la superficie.
Lo mejor de la teoría de grafos es que se puede utilizar en multitud de problemas. Piénsalo, existen muchas situaciones que se pueden definir como una red de nodos conectados entre sí.
Aquí te traigo 3 ejemplos concretos donde se usa.
Optimización de rutas
En el problema del viajante de comercio (sí, el TSP que ya hemos visto en alguna ocasión) podemos definir las ciudades como nodos y los caminos para ir de una ciudad a otra como las conexiones entre dichos nodos.
Si a cada conexión le añadimos como peso la distancia o el tiempo que se tarda en ir de una ciudad a otra… Ya tenemos nuestro grafo.
Lo que querremos después es utilizar un algoritmo de optimización para encontrar la ruta más corta, y ahí podemos usar el algoritmo de Dijkstra, por ejemplo.
Detección de fraude
Las instituciones financieras utilizan la teoría de grafos para detectar transacciones fraudulentas.
Modelan la red de transacciones, con las cuentas como nodos y las transacciones como aristas.
Los algoritmos de grafos pueden identificar patrones sospechosos, como grupos de cuentas con actividad inusual o picos repentinos en las transacciones.
Al analizar estas conexiones, pueden detectar actividad fraudulenta y prevenir pérdidas financieras.
Asignación de recursos y planificación
La asignación eficiente de recursos y la planificación de tareas son críticas en ciertas industrias como la construcción o la manufactura. Las empresas buscan optimizar el uso de recursos como maquinaria o personal mientras cumplen con los plazos del proyecto y minimizan los costos.
En este caso podríamos tratar las tareas o eventos de un proyecto como los nodos del grafo, mientras que las aristas representarían las dependencias entre ellas.
Usando técnicas como el Método del Camino Crítico (CPM, del inglés Critic Path Method) se puede identificar la secuencia más larga de tareas que determina el tiempo mínimo de finalización del proyecto.
Al enfocarse en optimizar el camino crítico, las empresas pueden asignar recursos de manera más eficiente, acelerar la finalización del proyecto y reducir los costes asociados con los retrasos.
Estos son solo 3 ejemplos, pero hay muchísimos más. Una opción interesante si quieres indagar más en teoría de grafos es la Revista de Teoría de Grafos, donde hay muchos artículos de acceso abierto interesantes.
Y si quieres toquetear algo práctico, una librería de Python con muchísimas funcionalidades es NetworkX. Tiene una muy buena documentación y es perfecta para aprender y aplicar conceptos de teoría de grafos, e incluso resolver problemas de optimización con algunos de sus módulos.
🏁 Algunas conclusiones
No sé si Cristiano Ronaldo se esperaba esto.
De ser uno de los influencers de Twitter a que de repente Macaulay Culkin, con casi 110 millones menos de seguidores, pueda ser más importante que él.
La teoría de grafos nos ha enseñado hoy varias cosas, como que:
Una red social es un grafo que representa relaciones entre nodos
Dentro de una red social hay nodos que son más importantes que otros
No hay una única manera de medir la importancia de los nodos más críticos
Los grafos son una herramienta súper útil para resolver problemas de negocio
Ahora, cada vez que veas relaciones entre diferentes personas, proyectos o tareas verás un grafo ahí, será inevitable.
Pero si lo has hecho ya en alguna ocasión… ¿Qué problemas has resuelto ya utilizando la teoría de grafos? ¿Por qué decidiste hacerlo así? ¿Qué algoritmos has usado para ello? Cuéntamelo en comentarios!
Nos vemos la semana que viene.
Un abrazo,
Borja.
PD: si quieres ver el programa de TVE en el que me he inspirado para este post, se llama Una Matemática Viene a Verme y lo tienes aquí. Clara Grima, matemática a quien te recomiendo encarecidamente seguir, habló muy bien sobre viralidad en redes.