📈 #17 Resuelve problemas complejos de manera sencilla con metaheurísticas
Conquista sin esfuerzo los desafíos de optimización con estrategias simplificadas
Sinceramente, no creí llegar a este tema tan pronto, pero aquí estamos. Esta semana en Factibles te quiero hablar de metaheurísticas:
Ventajas
Limitaciones
2 ejemplos concretos
La razón principal es que los algoritmos exactos son los más típicos a la hora de resolver problemas de optimización, pero tienen un pequeño gran inconveniente: hay una clase de problemas con interés práctico para los que no se conocen algoritmos exactos con tiempos de ejecución razonables que hacen que aunque exista algoritmo para encontrar soluciones, necesitarías demasiado tiempo para resolverlos.
Y se necesitan otras técnicas, claro.
Una vez las conoces, se abre un mundo nuevo de posibilidades a la hora de resolver problemas de optimización.
De hecho, yo mismo empecé justo en este punto y fue lo que me enganchó al mundillo. Pero eso es otra historia. Ahora…
¡Vamos a por ello!
Desde que empecé a hablar de heurísticas hace unas semanas hasta ahora, casi sin darte cuenta has ido avanzando en técnicas más avanzadas. El camino era claro:
Heurísticas → Búsqueda Local → Metaheurísticas
Y se entiende mejor así porque estas últimas técnicas -las metaheurísticas- se apoyan en conceptos anteriores, mejorando las soluciones encontradas con las técnicas que ya te he presentado.
Pero, ¿qué es una metaheurística?
Procedimiento maestro de alto nivel que guía y modifica otras heurísticas para explorar soluciones más allá de la simple optimalidad local.
Fred Glover, Future paths for integer programming and links to artificial intelligence. Computers and Operations Research, 13:533 549, 1986.
Básicamente, funcionan haciendo evolucionar a una solución o un conjunto de soluciones de manera iterativa hasta que se considera que es tan buena que se dejan de buscar otras soluciones.
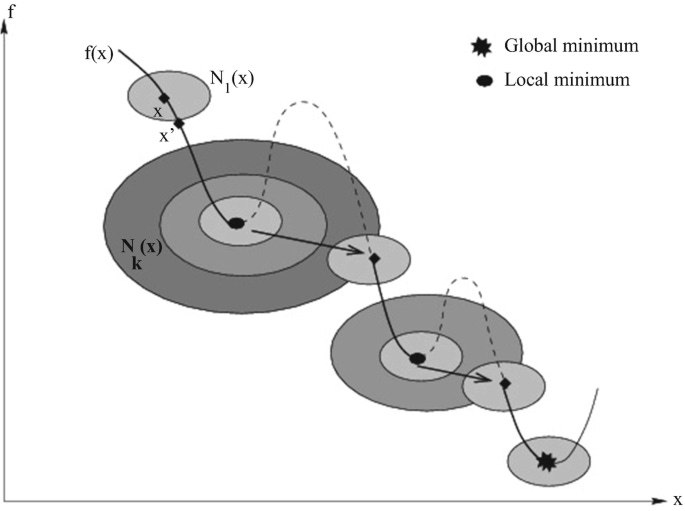
Cuando te hablé de procedimientos de búsqueda local, vimos que una búsqueda local se queda atrapada en un óptimo local. Pues bien, la metaheurística viene a solucionar ese problema: es capaz de moverse en el espacio de soluciones para encontrar una mejor solución.. Y lo hace gracias a un concepto clave.
Seguro que te suena eso de de exploración vs explotación que tanto se comenta en Inteligencia Artificial (especialmente en Reinforcement Learning)… Pues justo eso es lo que hacen las metaheurísticas. Yo siempre lo he conocido como diversificación vs intensificación, pero es exactamente el mismo concepto:
Diversificación: la idea de moverte en el espacio de soluciones para encontrar soluciones diferentes entre sí.
Intensificación: la idea de explorar de manera intensiva un área concreta del espacio de soluciones para encontrar un óptimo local.
Así que te dejo por aquí sus ventajas, limitaciones y un par de metaheurísticas.
🚀 Ventajas
Las metaheurísticas presentan dos principales ventajas frente a otras heurísticas / búsquedas locales, pero también frente a algoritmos exactos. Son como la intersección ideal entre la búsqueda local y los algoritmos exactos.
🔝 Son capaces de proporcionar soluciones de alta calidad…
Con una metaheurística serás capaz de escapar de un óptimo local, moverte por el espacio de soluciones -diversificación- y encontrar una mejor solución -intensificación-.
Dependiendo de la metaheurística, tenderá más a tener procesos determinísticos -que te permiten intensificar- o estocásticos -que te permiten diversificar-.
Encontrar ese balance entre diversificar e intensificar es clave para encontrar buenas soluciones al problema de optimización al que te enfrentes.
⌛ …en poco tiempo de ejecución
Las metaheurísticas destacan precisamente por encontrar ese balance entre diversificación e intensificación de manera bastante eficiente.
⭐ Además, son especialmente útiles cuando:
El problema es difícil de expresar en un modelo matemático, por lo que resolverlo de manera más tradicional (con un solver) se hace muy, muy difícil.
Un método tradicional tarda demasiado tiempo en ejecutar por la complejidad del problema en sí mismo, y se necesita una solución en un tiempo acotado.
🧩 Limitaciones
Ojo, que no todo el monte es orégano. Trabajar con metaheurísticas también tiene sus retos. Hay varios retos principales a los que te enfrentas cuando resuelves un problema de optimización de esta manera.
🎯 El primero de ellos es la optimalidad. Con una metaheurística no sabes si la solución es óptima o no. En problemas donde esto es crucial, no te aconsejaría nunca usar una metaheurística de manera aislada, aunque igual tiene sentido combinada con métodos exactos para tener un muy buen punto de partida de búsqueda de la solución óptima.
🤓 Por otra parte, para aprovechar el máximo potencial de las metaheurísticas necesitas tener un conocimiento profundo del problema. Es en ese momento cuando puedes generar estrategias de búsqueda de soluciones eficientes. Y claro, llegar a ese conocimiento específico hace que inviertas mucho tiempo en desarrollo. Todo esto provoca que todo ese conocimiento adquirido y las técnicas empleadas para resolver tu problema pueden no servirte en otros problemas.
🔢 Por último, hay que tener en cuenta que las metaheurísticas tienen parámetros que configurar. Unas más, y otras menos. Unas tienen parámetros más sencillos o entendibles, y otras más complicados. Por eso, también se hace necesario hacer una búsqueda de los parámetros que mejor le vienen para resolver tu problema. Si conoces métodos como Grid Search o Random Search, el concepto es exactamente el mismo: iterar sobre valores de los diferentes parámetros hasta encontrar la combinación adecuada que te permite minimizar tiempos de ejecución y encontrar soluciones de mayor calidad.
📸 Ejemplos
Metaheurísticas hay muchas. Unas basadas en mejorar una única solución y otras basadas en poblaciones de soluciones. Unas basadas en búsqueda local y otras en combinaciones de soluciones. Unas basadas en búsqueda multi-arranque y otras basadas en estimaciones de distribuciones estadísticas.
Cada una tiene sus puntos fuertes y sus debilidades, y unas obtendrán buenas soluciones a tu problema y otras igual no tanto.
Escoger una en concreto para resolver tu problema es muy complicado.
Por eso, la mejor estrategia es prototipar 2-3 diferentes y ver qué funciona mejor, para después dedicar más esfuerzos a aquellas estrategias que mejor funcionen.
Así que aquí te voy a presentar 2 metaheurísticas muy diferentes entre sí, para que entiendas sus diferencias y empieces a aplicarlas en tu próximo problema.
🧬 Algoritmos genéticos
Son algoritmos basados en la idea neo-darwiniana de evolución de las especies. Se desarrollaron a mediados de la década de 1970 por John H. Holland -aunque se pueden encontrar versiones más modernas, como esta-, y vienen inspirados por los algoritmos evolutivos que comenzaron su desarrollo a finales de la década de 1950.
Si te preguntabas por qué son tan famosos estos algoritmos, ya sabes una de las razones, y es que son muy antiguos.
Como dicen los ingleses: old but gold.
Esta idea neo-darwiniana de evolución se puede expresar de la siguiente manera:
Los individuos que tienen una mejor adaptación al medio tienen una probabilidad más elevada de vivir más tiempo, con lo que tendrán más posibilidades de generar descendencia que herede sus buenas características.
En cambio, los individuos con peor adaptación al medio tienen menos probabilidad de sobrevivir, por lo que tendrán menos oportunidades de generar descendencia y probablemente acaben extinguiéndose.
Desde un punto de vista completamente algorítmico tendríamos que estas metaheurísticas son:
Poblacionales, dado que operan con un conjunto de soluciones llamadas individuos.
De combinación de soluciones, dado que es típico escoger pares de individuos -los padres- para combinarlos y generar una nueva solución -hija- que tendrá características buenas de esas soluciones combinadas. También es típico hacer movimientos de mutación, donde un individuo cambia solo una parte de sí mismo, mutando.
De inspiración evolutiva, por lo que es más que evidente.
🏘️ Búsqueda de Vecindad Variable (o VNS, del inglés Variable Neighborhood Search)
Esta es una metaheurística relativamente nueva, sobre todo comparada con los algoritmos genéticos. Aquí, además, nos encontramos con una metaheurística muy diferente porque es:
Trayectorial, o lo que es lo mismo, solo opera con una única solución que va evolucionando con el tiempo.
Basada en búsqueda local, ya que utiliza métodos de búsqueda local para intensificar y encontrar óptimos locales.
Por entornos, ya que utiliza diferentes estructuras de vecindad para encontrar esas soluciones óptimas.
Se basa en tres puntos concretos:
Un óptimo local respecto a una vecindad no tiene por qué serlo respecto a otra.
Un óptimo global es un óptimo local respecto a todas las posibles estructuras de vecindad.
Para muchos problemas, los óptimos locales con respecto a una o varias estructuras de vecindad están relativamente cerca.
Esto último, por supuesto, es una observación empírica, pero implica que en ocasiones un óptimo local nos ayuda a entender cierta información sobre el óptimo global.
Puedo afirmar y de hecho afirmo que VNS es mi metaheurística preferida 😍 He trabajado mucho con ella, haciendo implementaciones de todo tipo: hibridándola con otras metaheurísticas, con estrategias multi-arranque, paralelizando su ejecución… Y es que tiene dos puntos muy fuertes:
Es súper flexible
Apenas necesita parametrización
Te cuento más sobre ella en futuros posts 😉
🏁 Conclusiones
Era necesario, pero es que hoy te he contado muchísimo…
Qué son las metaheurísticas
Ventajas y limitaciones que tienen
2 metaheurísticas muy famosas, una con historia y otra con 2 puntos fuertes muy interesantes
Pero es que esto no acaba aquí, esto es solo la punta del iceberg! Podemos profundizar mucho y hablar de cada tipo de metaheurísticas, o hablar de paralelización para ejecutarlas más rápidamente, o de su futuro con las hiper-heurísticas y mat-heurísticas, o incluso el futuro de la optimización con Reinforcement Learning o Computación Cuántica…
Dime tú: ¿por dónde quieres que te siga contando cosas?
Un abrazo,
Borja.